Chapters
A list of numbers can be arranged in an arithmetic, geometric, Fibonacci, or harmonic sequence. In this article, you will learn what is an arithmetic sequence, how to calculate its nth terms, and how to find the sum of the sequence up to the n number of terms.

What is an Arithmetic Sequence?
An arithmetic sequence represents the series of numbers arranged in a specific pattern. If the numbers are arranged in an arithmetic sequence, and you take any number in the list and subtract its predecessor, the resulting number will always be the same. This number that you obtain after subtracting the previous number from the next number is known as a common difference and is denoted by d. The common difference is used to determine the next terms in the series. You just add the common difference to any term in the list to get the next term.
An arithmetic sequence can be:
- Increasing: If the common difference is positive, then we say that the sequence is increasing.
- Decreasing: If the common difference is negative, then we say that the sequence is decreasing.
An arithmetic sequence is also known as arithmetic progression. We can summarize the above information about the arithmetic sequence in this way:
A list of numbers arranged in such a way that the difference between two successive terms is a constant d is known as an arithmetic sequence
Now, the next step is to calculate the sum of the first 50 terms in the series. We will use the following formula to calculate the sum:
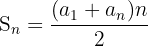
Substitute 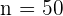 ,
, 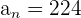 , and
, and 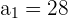 in the above formula to get the sum:
in the above formula to get the sum:
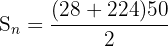
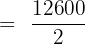
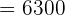
Hence, the sum of the sequence upto the 50th term is 6300.
Now, the next step is to calculate the sum of the first 48 terms of the series. We will use the following formula to calculate the sum:
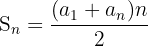
Substitute  ,
,  , and
, and 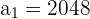 in the above formula to get the sum:
in the above formula to get the sum:
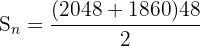
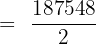
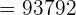
Hence, the sum of the sequence upto the 48th term is 93792.
Now, the next step is to calculate the sum of the first 35 terms of the series. We will use the following formula to calculate the sum:
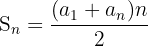
Substitute 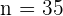 ,
, 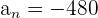 , and
, and 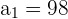 in the above formula to get the sum:
in the above formula to get the sum:
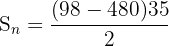
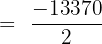

Hence, the sum of the sequence upto the 35th term is -6685.










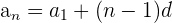
 and n = 50 in the above formula to get the 50th term.
and n = 50 in the above formula to get the 50th term.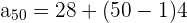

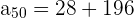
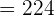
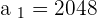 and n = 48 in the above formula to get the 48th term.
and n = 48 in the above formula to get the 48th term.

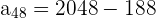

 and n = 35 in the above formula to get the 35th term.
and n = 35 in the above formula to get the 35th term.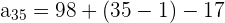
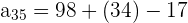
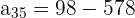
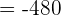



I have math qstn problm
Break even point