Chapters

Exponent
| Exponent | |
| Definition | 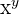 |
| Other Names | Power, index |
| Written Out | ‘x to the power of y’ |
| Expanded | 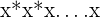 |
| Example | 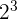 = 2x2x2 = 8 = 2x2x2 = 8 |
As you can see, exponents can be quite powerful. It allows us to be able to multiply on a large scale. When you work with exponents, you are usually working with large numbers. This is because, as you multiply a number by itself over and over again, it grows very quickly.
Take a look at the example below, using just one number. Notice how quickly the result becomes a large number.
| Result | |
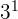 | 3 |
 | 9 |
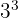 | 27 |
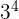 | 81 |
 | 243 |
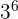 | 729 |
While there is little difference between 3, 9 and 27 - the difference between 243 and 729 is significant.
Exponent Rules
There are many rules and properties that can be helpful to remember when dealing with exponents. The first, most basic rule, is that the ‘y’ term tells you how many times to multiply x by itself.

While it’s easy to see what to do when we have a positive number, what happens when we have a negative number or fraction as a power?
| Form | Rule | Example | Result | |
| Negative |  | 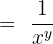 | 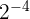 | 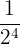 = = 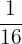 |
| Fraction | 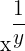 | 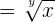 | 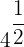 | 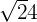 = 2 = 2 |
For more complex fractions, we simplify the fraction until we can get a number multiplied by a fraction with a numerator of 1.

Take the following as an example.
| Rule | Result | |
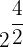 | 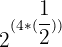 | 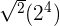 = =  = 4 = 4 |
The best powers to have are 0 and 1 because the rules for those are easy.
| Form | Result | Example | |
| 0 | 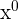 | 1 | 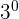 = 1 = 1 |
| 1 | 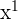 | x | 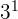 = 3 = 3 |
Exponential Function
An exponential function is a function that has an exponent in it. When we have an exponent in a function, this means that the function takes on the following general form:
As you can see, there are some elements to this function. Below, we break down each element in the function.

| y | Result, the dependent variable |
| a | Constant term |
| x | Input, the independent variable |
Exponential functions are used in many different branches in math. They are very powerful functions. Let’s take a look at an example exponential function:

| x | y |
| -1 | 0.33 |
| -0 | 1 |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
Exponential Function Properties
When you’re working with exponential functions, it is important that you understand that they have several exponential properties. Take a look at the table below to learn more about the properties that exponential functions have.
| Property 1 | The input variable, or independent variable, is in the power position. This is very different from regular functions. |
| Property 2 | Exponential relationships decrease or increase very fast. The first couple inputs are much closer than later ones. |
| Property 3 | Always contains point (0,1), because regardless of what a is, any number to the 0 power is always 1 |
Exponential Growth
When using exponential functions, the most common relationship they model is one called exponential growth. Exponential growth happens when something grows at an exponential, or increasingly fast, rate. The spread of the coronavirus is one current example of that.

The image is an example of a very simple exponential growth function, which is written below:
\[
y = 5^{x + 3} + 5
\]
As you can see, the first two values are pretty close. When x = -3, y is equal to 6. On the other hand, when x = -2, y is equal to 10. Compare this to x = 1 and x = 2, where the y is equal to 630 then 3130, respectively. The difference between 6 and 10 is a lot smaller than the difference between 530 and 3130.
Exponential Decay
When using exponential functions, the other most common relationship they model is one called exponential decay. Exponential decay happens when something decays at an exponential, or increasingly fast, rate. The rate of decomposition of radioactive elements is an example of exponential decay.

As you can see, the formula for exponential decay differs from that of exponential growth in that we have a negative exponent. Take a look at one example:
\[
y = 3^{-x}
\]
If we plug in values from -3 to 3, you can see the behaviour with this function is similar to the exponential growth function. At -3, we get a y equal to 27. At x = -2, we get a y of 9. Compare this to the y’s at x = 1 and x = 2.
Notice that the decay happens rapidly at first, where the difference between the first two points is a lot more than the difference at points 1 and 2.
Example 1
In this example, we’ll look at how to graph an exponential function. The first step in graphing an exponential function is to examine the function.
\[
f(x) = 8^x
\]
As you can see, it is clear that it is exponential because the independent variable is in the power. Next, we simply plug in values for x. Check out some sample values below.
| x | y |
| -3 | 0.00 |
| -2 | 0.02 |
| -1 | 0.13 |
| 0 | 1.00 |
| 1 | 8.00 |
| 2 | 64.00 |
| 3 | 512.00 |
Example 2
Let’s graph the following exponential growth function:
\[
f(x) = 4^{x+2} + 6
\]
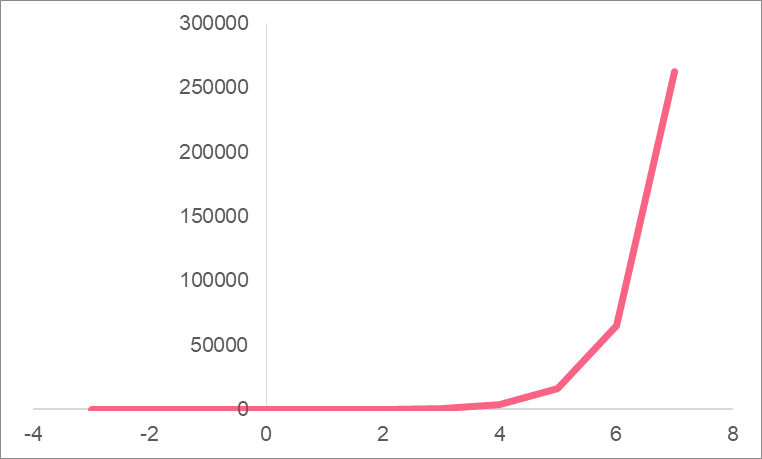
As you can see, you can plot any points, as long as you follow the function.
Example 3
For this problem, let’s look at exponential decay and see how it is different from exponential growth. Let’s plot the following function:
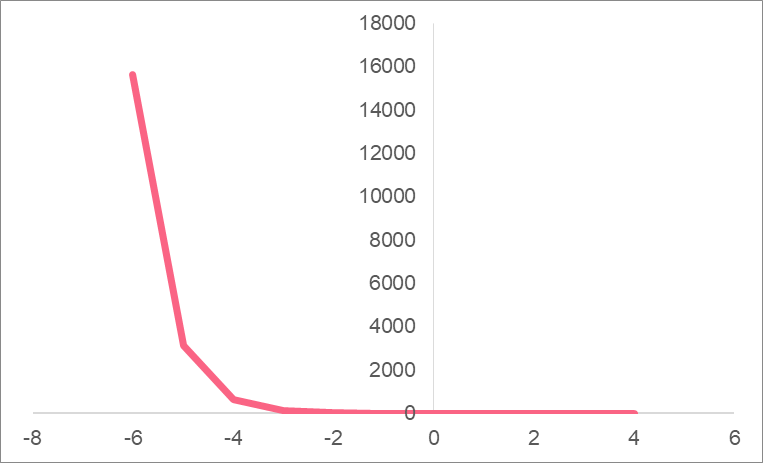
As you can see, this is exactly the opposite of what we experience in an exponential growth. Take a look at the points below, as well as the differences between the points.
| x | y | Difference |
| -6 | 15625 | |
| -5 | 3125 | 15625-3125 = 12500 |
| ... | ... | ... |
| 3 | 0.008 | |
| 4 | 0.0016 | 0.008 - 0.0016 = 0.0064 |













I have math qstn problm
Break even point