What is a Rational Function?
A rational function can be defined as:
"A ratio of two polynomials"
Or
"When one polynomial is divided by another polynomial, we get a new function known as a rational function"
We call it a "Rational" function because it is a ratio of two polynomials. Remember that the polynomial in the denominator cannot be zero.
Examples of Rational Functions
Some examples of rational functions are given below:
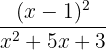
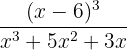
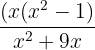
Graphing Rational Functions
It can be difficult to sketch the graphs of rational functions. However, once you know the asymptotes and intercepts of the function, it becomes fairly simple to draw a graph. Follow the steps below to graph a rational function: Step 1 - If there are asymptotes of a rational function, find them in the first step. Use dotted lines to draw asymptotes. Note that the graph may cross a horizontal asymptote, but it should never cross a vertical asymptote. Step 2 - Find vertical intercepts of the rational function Step 3 - Find horizontal intercept of the function Step 4 - Use many values of x to find different y values Step 5 - Plot the points in a xy-plane and join the points to draw a smooth curve. Remember that your graph should not cross the vertical asymptotes.
How to Find Asymptotes and Intercepts?
Now, the question arises how to find the asymptotes and intercepts of a rational function? Well, we can find the vertical asymptote of the function by setting a denominator equal to zero and solving the function for x. To find horizontal asymptotes, look at the degree of the polynomial in the numerator. If it is greater than the degree of the denominator, then we can say that the function has no horizontal asymptote. On the other hand, if the degrees of the numerator and the denominator are the same then we find the horizontal asymptote by dividing the leading coefficients of the rational function. The horizontal asymptote of the function is 0 if the degree of numerator is less than that of the denominator. After finding the asymptotes, you need to find out the x and y intercepts. By substituting x = 0, we can get the vertical intercept. For the horizontal intercept, you can isolate x on the left-hand side and set the function equal to 0 to find the value of x. The concept of graphing rational functions will become more clear in the following examples:
Example 1
Graph the following function:
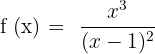
Solution
We will graph the above rational function by following the steps below: Step 1 - Find the asymptotes of the function To find the vertical asymptote of the function we need to set the denominator of the function equal to zero. The vertical asymptote is the line which the graph cannot cross because when the denominator becomes zero, the function is undefined.
Hence, the vertical asymptote of the function is 1. To find the horizontal asymptote of the rational function, we look at the degree of the polynomial in the numerator. If it is greater than the degree of the polynomial in the denominator, then we can say that the function has no horizontal asymptote. In this example, the numerator has a greater degree than the denominator, therefore, we can say that this function has no horizontal asymptote. Step 2 - Find the vertical intercept Let us find the vertical intercept of the function by substituting x = 0.
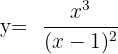
Hence, the vertical intercept of the function is (0, 0). Step 3 - Find the horizontal intercept We will calculate the horizontal intercept by setting the function equal to zero.
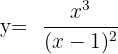
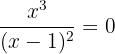
The horizontal intercept of the function is also (0,0). Step 4 - Use many values of x to find different y values In this step, we will use many values of x to find several different values of y. Lets start by substituting numbers in the function:
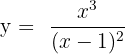
At x = 2, y = 8 At x = 3, y =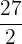
At x = -1, y =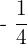
You can plot many points like above to sketch the graph. Step 5 - Plot the points in an xy-plane and join the points to draw a smooth curve. After plotting the above points and drawing the asymptote with a dotted line, we get the following graph: 
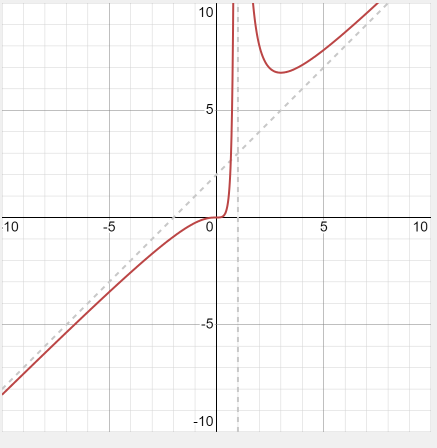
Example 2
Graph the following function:
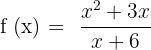
Solution
We will graph the above rational function by following the steps below: Step 1 - Find the asymptotes of the function To find the vertical asymptote of the function we need to set the denominator of the function equal to zero. The vertical asymptote is the point from which the graph will not pass because when the denominator becomes zero, the function becomes undefined.
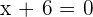
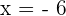
Hence, the vertical asymptote of the function is -6. To find the horizontal asymptote, look at the degree of the polynomial in the numerator. In this example, the numerator has a greater degree than the denominator, therefore the function has no horizontal asymptote. Step 2 - Find the vertical intercept First, let us find the vertical intercept of the function by substituting x = 0.
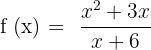
Hence, the vertical intercept of the function is (0, 0). Step 3 - Find the horizontal intercept We will calculate the horizontal intercept by setting the function equal to zero.
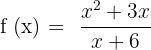
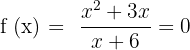
The horizontal intercept of the function is also (0,0). Step 4 - Use many values of x to find different y values In this step, we will use many values of x to find several different values of y. Lets start by substituting numbers in the function:
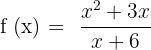
At x = 2, y =
At x = 3, y = 2 At x = 1, y =
Plot many points like above to get the graph. Step 5 - Plot the points in an xy-plane and join the points to draw a smooth curve. After plotting many points and drawing the asymptote with a dotted line, we get the following graph: 
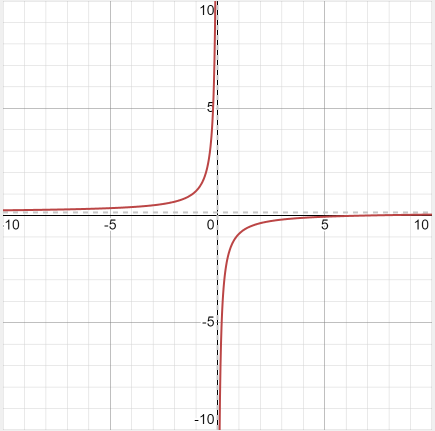
Example 3
Graph the following function:
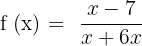
Solution
We will graph the above rational function by following the steps below: Step 1 - Find the asymptotes of the function To find the vertical asymptote of the function we need to set the denominator of the function equal to zero. The vertical asymptote is the point from which the graph will not pass because when the denominator becomes zero, the function becomes undefined.
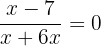
Hence, the vertical asymptote of the function is 0. To find the horizontal asymptote, look at the degree of the polynomial in the numerator. In this example, the degree of the numerator is equal to the degree of the polynomial in the denominator, hence after simplifying the expression like we will divide the leading coefficients of the numerator and the denominator to get the horizontal asymptote:
Horizontal asymptote = 
Step 2 - Find the vertical intercept We usually find the vertical intercept of the function by substituting x = 0. But the function in this example, we cannot substitute x = 0 because the function will become undefined. Hence, we can say that this function has no y-intercept.
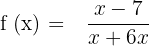
Step 3 - Find the horizontal intercept We will calculate the horizontal intercept by setting the function equal to zero.
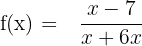
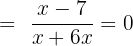
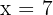
The horizontal intercept of the function is also (7,0). Step 4 - Use many values of x to find different y values In this step, we will use many values of x to find several different values of y. Lets start by substituting numbers in the function:
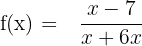
At x = 2, y =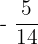
At x = 1, y =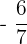
At x = 3, y =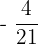
Plot as many points as you can like shown above to get the graph. Step 5 - Plot the points in an xy-plane and join the points to draw a smooth curve. After plotting the points and drawing the asymptote with a dotted line, we get the following graph: 
Summarise with AI:
Did you like this article? Rate it!
Loading...
I get it somehow, there are others who are unfamiliar and I have a hard time with it but it’s okay that I get it.
Thanks for sharing your thoughts! It’s completely normal to find some parts unfamiliar or more difficult than others. The important thing is that you’re making progress and understanding more as you practise. Keep going! 😊
At least I understood some of it, but there are others that I’m confused about and have a hard time understanding, but I get it.
Thanks for sharing! It’s great that you’ve understood some of it already. Don’t worry if a few parts are still confusing — keep practising and take your time with the trickier sections. You’ll get there! 😊
The lesson was a little difficult for me, especially the word problems, but the examples helped me understand it better.
Thanks for your feedback! Word problems can definitely be tricky, so we’re glad the examples helped make the lesson clearer. Keep practising — it gets easier with time! 😊
Thankyouuu po