Chapters
Everything in this world has a specific equation. It can be any type of equation, whether just a simple algebraic equation or maybe a complex differential equation. That is not our concern, for now, what matters is that maths is all around. The chair you are sitting in has a mathematical equation, the coffee you are drinking has an equation, the air and light in your surrounding also have a specific mathematical equation. The question is, how do we relate all of this? How do we know which equation is of the light and which equation is of the coffee? The simplest solution is to call them in functions!
You might be wondering what is a function now? A real function of real variables is any function, f, that associates to each element of a certain subset (domain), another real number (image). In simple words, a function is a law, expression, even a rule that connects one variable to another variable. For example, we have an equation, 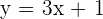 , where y is a dependent variable while x is an independent variable. It means that y will always depend on the value of x. Let's make a function,
, where y is a dependent variable while x is an independent variable. It means that y will always depend on the value of x. Let's make a function,  , the function is relating input to the output. Whatever value you will input, the function will relate it with the output. In simple words, when you input the value to a function, it will show you that for that specific input, this will be the output.
, the function is relating input to the output. Whatever value you will input, the function will relate it with the output. In simple words, when you input the value to a function, it will show you that for that specific input, this will be the output.
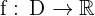

The subset which defines the function is called the domain.
The number x belonging to the domain of the function is called the independent variable.
The number, y, associated for f to the of value x, is called the dependent variable. The image of x is designated by f(x):
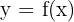
The range of a function is the set of real values that takes the variable y or f(x).
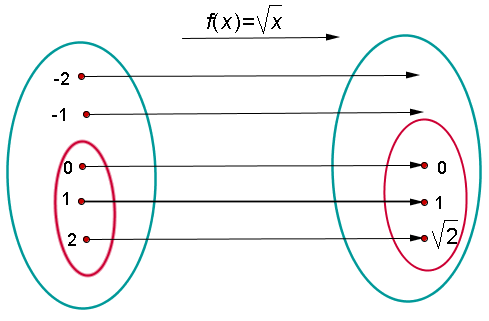
Initial set Final set
Domain Range
The domain is the set of elements that has an image.
D = {x 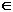

The range is the set of the images.
R = {f(x)/x 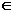

Graph of a Function
If f is a real function, every pair 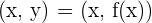 determined by the function f corresponds to the Cartesian plane as a single point
determined by the function f corresponds to the Cartesian plane as a single point 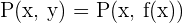 . The value of x must belong to the domain of the definition of the function.
. The value of x must belong to the domain of the definition of the function.
The set of points belonging to a function is unlimited and the pairs are arranged in a table of values that correspond to the points of the function. These values, on the Cartesian plane, determine points on the graph. Joining these points with a continuous line gives the graphical representation of the function.
 |  |  |  |  |  |
|---|---|---|---|---|---|
 |  |  |  |  |  |
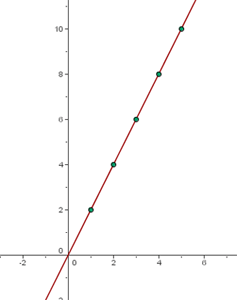
Example
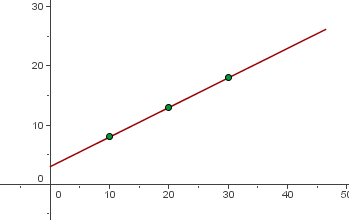
The price of a taxi ride is represented by: 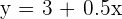 . Where x is the time in minutes of the ride.
. Where x is the time in minutes of the ride.
 |  |  |  |
|---|---|---|---|
 |  |  |  |












I have math qstn problm
Break even point