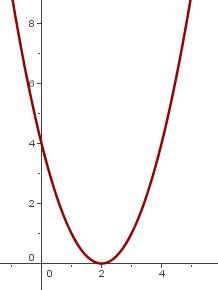
Graphing parabola is a bit complex and that is why we made a separate resource for it. To graph a parabola, it is important to understand all the fundamental concepts of parabolas that include everything such as equations, solutions, and a few more. In this lesson, you will understand how parabolas are positioned on graphs by changing their equation and how you can predict their position.
Equation: 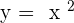
| x | y = x² |
|---|---|
| -2 | 4 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 4 |
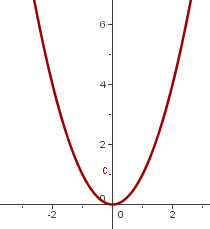
Above is a graph of parabola with just a simple equation. That equation is the basic equation of a parabola. It means that its vertex lies in the origin of the graph and the line of symmetry is at  . However, when we are graphing or plotting parabola graphs, our equation usually has constants (which we will discuss later in this resource) but here, all the constants are zero leaving
. However, when we are graphing or plotting parabola graphs, our equation usually has constants (which we will discuss later in this resource) but here, all the constants are zero leaving 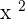 alone and that is why this graph is like a U-shape graph. A parabola will always be drawn like above if all the constants are zero in the equation.
alone and that is why this graph is like a U-shape graph. A parabola will always be drawn like above if all the constants are zero in the equation.

1. Vertical Translation
Equation: 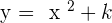
Let's say you want to shift the parabola vertical, to shift that parabola, we need the help of a constant. Since the equation is already in terms of y hence most of our work is already done. All you need to do is to add a constant at which you want to shift. For example, we want to shift a parabola having vertex  to
to 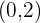 . It means we are lifting the parabola from origin to a new value, in short, we are lifting it vertically. To shift it on
. It means we are lifting the parabola from origin to a new value, in short, we are lifting it vertically. To shift it on 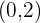 , you need to put the value of k equal to
, you need to put the value of k equal to  . Hence, the equation will be:
. Hence, the equation will be:
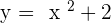


y = x² + 2y = x ² - 2
In Nutshell
If k > 0, 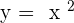 moves upward k units.
moves upward k units.
If k < 0, 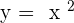 moves down k units.
moves down k units.
The vertex of the parabola is: 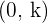 .
.
The axis of symmetry is:  .
.
2. Horizontal Translation
What if you want to shift your parabola in the horizontal direction? To do that, there is a little bit complex. One thing is for sure, you need to add in the x-component but the x-component in the equation is squared which means whatever numerical value that you want to add should be added to the x-component and then take a square of that number.

For example, you want to push the parabola from  to
to  on the x-axis. What you need to do is to add the numeric value "
on the x-axis. What you need to do is to add the numeric value " " to the x-component and then take a square of that. In simple words, replace the "h" in the above equation with "
" to the x-component and then take a square of that. In simple words, replace the "h" in the above equation with " ", however, the vertex of the parabola is
", however, the vertex of the parabola is 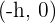 which means you need to change the sign of your value of h when you are plugging the value.
which means you need to change the sign of your value of h when you are plugging the value.


y = (x + 2)²y = (x − 2)²
In Nutshell
If h > 0, 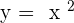 is shifted to the left h units.
is shifted to the left h units.
If h < 0, 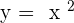 is shifted to the right h units.
is shifted to the right h units.
The vertex of the parabola is: 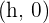 .
.
The axis of symmetry is: 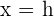 .
.
3. Oblique Translation
Last but not least, the oblique translation means to shift the parabola in horizontal as well as vertical direction. This means that to perform the oblique translation, you need to use both methods, the horizontal translation as well as the vertical translation. The equation for oblique translation is:
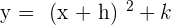
The vertex of the parabola is: 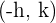
The axis of symmetry is:  .
.
For example, you have been asked by your teacher to shift the parabola from 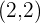 to
to 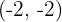 . There are two methods to do that, the first one is that first, you perform either horizontal translation or vertical translation and then you perform what is left. The second method is simple and fast which is to use the above equation. Do you remember
. There are two methods to do that, the first one is that first, you perform either horizontal translation or vertical translation and then you perform what is left. The second method is simple and fast which is to use the above equation. Do you remember  and
and  ? They are the same! "h" represents the translation on the x-axis while "k" represents the translation on the y-axis. All you need to do is to place the values in h and k but don't forget about the axis of symmetry. That is a key point!
? They are the same! "h" represents the translation on the x-axis while "k" represents the translation on the y-axis. All you need to do is to place the values in h and k but don't forget about the axis of symmetry. That is a key point!
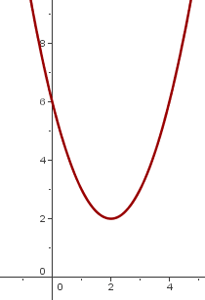
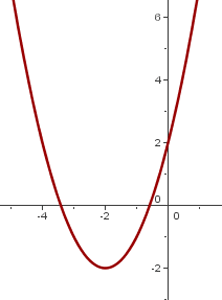
y = (x − 2)² + 2 y = (x + 2)² − 2












I have math qstn problm
Break even point