Chapters

Pattern
In calculus, many of the questions that you will encounter will ask you a question that relates to patterns in the function or numbers. In order to start discussing what ‘nth’ means, we should define a pattern.
A pattern is any sort of trend in a list of numbers, objects and more. Let’s take a look at some examples of patterns in math.

| A | Repetition |
| B | Even numbers |
| C | Odd numbers |
| D | Functions |
Sequence
The most common type of pattern in math is called a sequence. A sequence is a list of numbers that can be either finite or infinite.
| Infinite | Goes on forever | [1,5,9,.....) |
| Finite | Ends at a known number | [1,5,9,13] |
There are two special properties about sequences that go hand in hand. They can be seen below.
| Order | The order is important, you can’t switch up the order | [1,5,9,13] is not the same as [13,9,5,1] |
| Defined rule | A rule is defined for how to get each successive number | Rule for [1,5,9,13] is 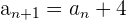 Rule for [13,9,5,1] is |
As you can see, sequences have specific notation that we can use to define the rules they use. These rules can also be called functions because they take one number as input and give an output.

Using the previous example, we can break down each element.
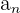 | The number at position n | The input |
 | The number at position n+1 | The output |
We pick 1 as a starting number. Because it is the first number in our list, it is located in position number 1.

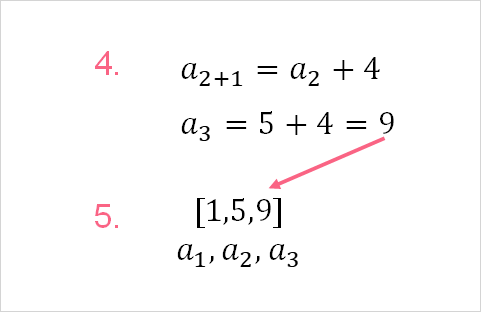
Our input is 1, which gives us 5. This number, at position 2, becomes the input for getting our next number at position 3.
The nth number is defined as the number n of any sequence. In this case, it would be 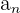 , which can be anything:
, which can be anything: 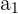 ,
,  ,
,  , etc.
, etc.
Arithmetic Sequence
There are many special types of sequences. Arithmetic sequences are a special type of sequence. It is defined as a sequence where every number has the same constant added to it. We already saw an example of this in the section before:
| Definition | Notation | Example | |
| Arithmetic Sequence | The same constant is added to every successive number |  | 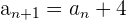 |
One common problem you’ll face is being asked to find the rule for a given sequence. One simple way to find the rule for a sequence is to first test whether a sequence is an arithmetic sequence.
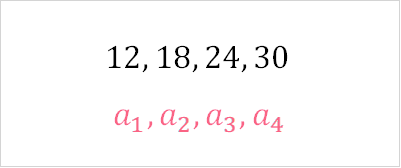
Using the sequence above, let’s test whether it is an arithmetic sequence. You can do this by the following steps.
| Step 1 | We need to take every number and subtract the one before it to see if they all result in the same constant |  |
| Step 2 |  | A |
| Step 3 | 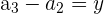 | B |
| Step 4 | 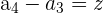 | C |
| Step 5 | Do all numbers match? | Does x = y = z ? |

Geometric Sequence
A geometric series is similar to an arithmetic sequence. The main difference is that, instead of adding a constant, we multiply each number by the same constant.
| Definition | Notation | Example | |
| Geometric Sequence | The same constant is multiplied to every successive number |  | 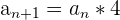 |
Now, instead of adding four, we multiply each nth number and 4. Let’s take a look at the first four numbers of this sequence starting with the number 3.

As you can see, from one number to the next, we have 4 multiplied. When you want to find out whether you have a geometric series or not, simply divide each successive number by each other.
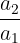 | 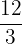 | 4 |
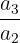 | 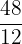 | 4 |
 |  | 4 |
Power
Powers define the number of times we multiply a number by itself. A power is also called a degree. The form that it takes is the following:

We can have many combinations of this. This is what ‘nth’ means when we talk about powers. The ‘nth’ power of a number is simply the number of times it is multiplied by itself. Take a look at a few examples below.
| 1 |  | 3*3 |
| 2 |  | 3*3*x |
| 3 |  | 3*3*x*x*x |
Square Root
You can think of a square root as the opposite of a power. The square root, or the root, of any function works to ‘undo’ a power. For example, let’s take the square root of 4.

As you can see, 2 to the power 2 is equal to 4. When we take the square root of a number, also called the 2nd root of a number, we want to find what number makes 4 when multiplied by itself two times.

As you can see, here the ‘nth’ root of a number is how many times one number multiplied by itself ‘n’ times fits into the number we’re taking the root of.
Polynomial Function
When we talk about polynomial functions and an ‘nth’ term, we usually mean the number of the observations. Say we have the following polynomial:

We get this formula from the following coordinates:
| x | y |
| 3 | 19 |
| 5 | 29 |
| 7 | 39 |
| 8 | 44 |
| 9 | 49 |
| 10 | 54 |
| 14 | 74 |
The nth value of x means that this value applies to any value of x within this range. For example, we can take the value of 2 for x and it results in: 14.










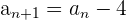



I have math qstn problm
Break even point