Chapters

Graph
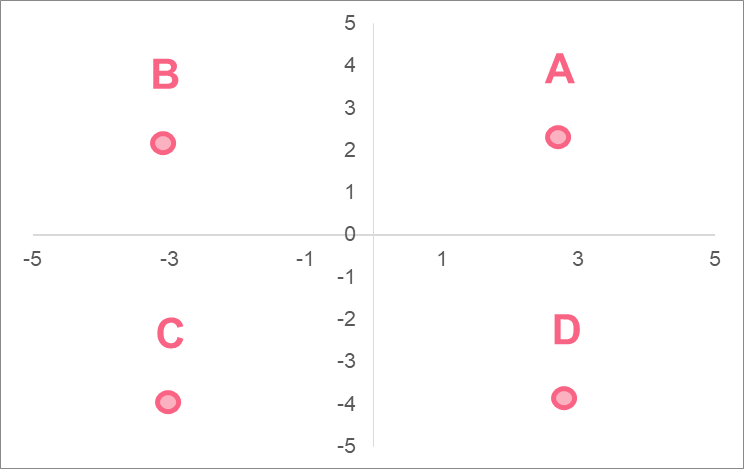
This represents a typical graph, where each point lies in a quadrant.
| Quadrant | Pattern | |
| A | Quadrant 1 | (positive, positive) |
| B | Quadrant 2 | (negative, positive) |
| C | Quadrant 3 | (negative, negative) |
| D | Quadrant 4 | (positive, negative) |
Notice that the quadrants always start at the top right and go counter-clockwise. Depending on what function we’re dealing with, we will have different resulting shapes.
Linear
A linear function is the most basic function. The function shows the linear relationship between an input and an output. The standard form is below.

We can find the slope of any line from any two points on the line. Take two points as an example.
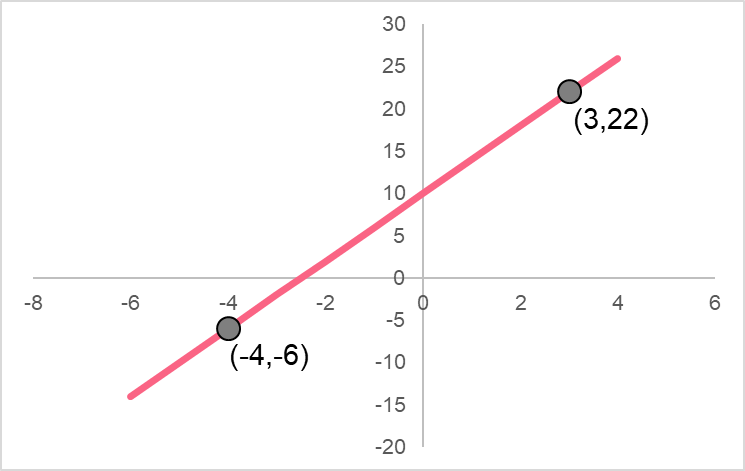
We would find it by following these steps.
| 1 | Put the points into the following formula. | m = 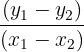 |
| 2 | Plug in the points into the formula | 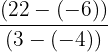 |
| 3 | Simplify | 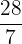 = 4 = 4 |
This gives us a slope of 4. The y-intercept, on the other hand, is easy to find. Since the y-intercept is the point where the line crosses the y-axis, it is whatever point on the line where x is 0.
Quadratic
A quadratic formula results in a parabola, which is shaped like a U. There are actually two common standard forms.
| Standard Form | Vertex Form |
f(x) = a + bx + c + bx + c | f(x) = a + k + k |
| Get the vertex point from converting to vertex form | The vertex is (h,k) |
Take a look at a parabola below. The vertex is the point on the parabola where, if we folded the parabola at that point, each side would be a mirror image of the other. The line where we ‘fold’ the parabola is called the axis of symmetry.

You can convert the standard form to the vertex form by:
- Completing the square
- Using the shortcut
The shortcut involves the following formula:

Here is an example:

Cubic
Cubic functions are one degree higher than quadratic functions. A degree is the power, or exponent, of a variable. Take a look at what a cubic function looks like.
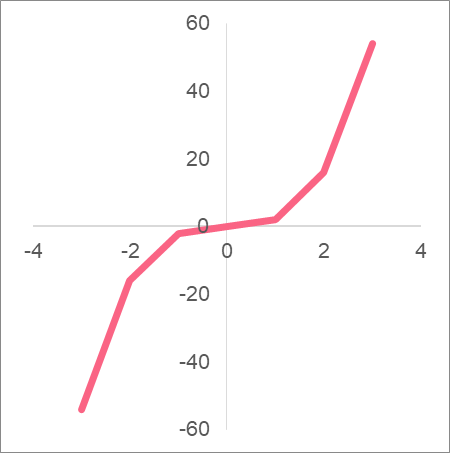
The standard form of a cubic function is the following.

The points a, b, c and d should all be real numbers. The only other rule to a cubic equation is that a should never be 0. If a is negative, the graph of the cubic function is flipped. Compare the two functions and their graphs below.

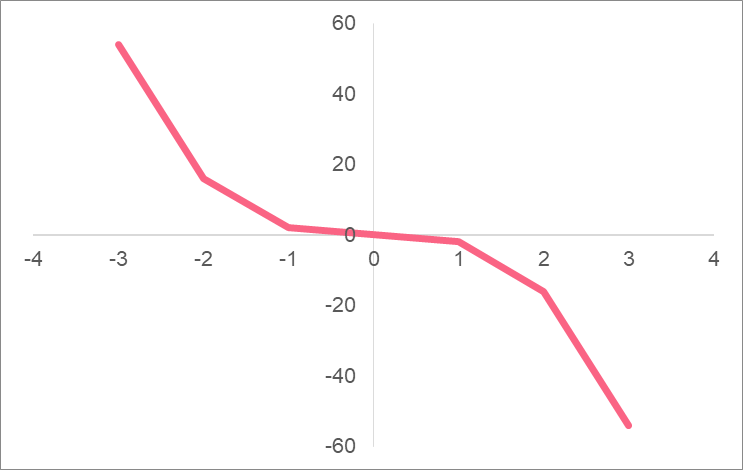
| A | B |
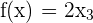 |  |
Exponential
An exponential function is one that models an exponential relationship. Take a look at the two most common formulas involving exponential growth and exponential decay.
| Formula | |
| Exponential growth |  |
| Exponential decay |  |
In an exponential relationship, one major property is that the graph always shows a sharp increase or decrease. In an exponential growth model, the points at the beginning of the graph are always closer than the points at the end.
It is the opposite for an exponential decay model. The points at the beginning of the graph are always further apart than those at the end. Take a look at the image below for an example.

Parabola
A parabola is modeled by a quadratic function. You’ve probably seen parabolas many times before: they are shaped like a ‘U.’ A quadratic function is a polynomial with a degree of two. The standard forms looks like the following:

As you can see, we have two ways of writing the equation of a parabola. When working with straight algebra, we usually use the ‘standard form.’ When working with parabolas, we use the ‘vertex form.’
This is because we can easily derive the vertex of the parabola, which is at point (h,k)
Problem 1
In this problem, you will have to use what you know about linear functions. Derive the slope of the line that goes through these two points:
- Point A: (1,7)
- Point B: (6, 27)
Problem 2
In this problem, you will have to use what you know about quadratic functions. Graph the following quadratic function:

Problem 3
In the previous problem, you were asked to graph a quadratic equation. You know that this function will give a parabola. State what the vertex of the parabola in Problem 2 is and mark it on the graph you drew.
Problem 4
In this section you were introduced to cubic functions. Without graphing the function, which one of the following graphs corresponds to the following function?
\[
2x^{3} + 3x
\]

Problem 5
In this problem, you will have to use what you know about linear functions. Derive the function of the line that goes through these two points:
- Point A: (2,5)
- Point B: (6, 7)
Problem 6
Transform the following quadratic equation to vertex form. After transforming it, plot the equation onto a graph.
\[
3x^{2} + 6x + 2
\]
Solution Problem 1
Here is how you derive the slope of the line that goes through these two points:
- Point A: (1,7)
- Point B: (6, 27)
\[
m = \frac{27-7}{6-1} = \frac{20}{5} = 4
\]

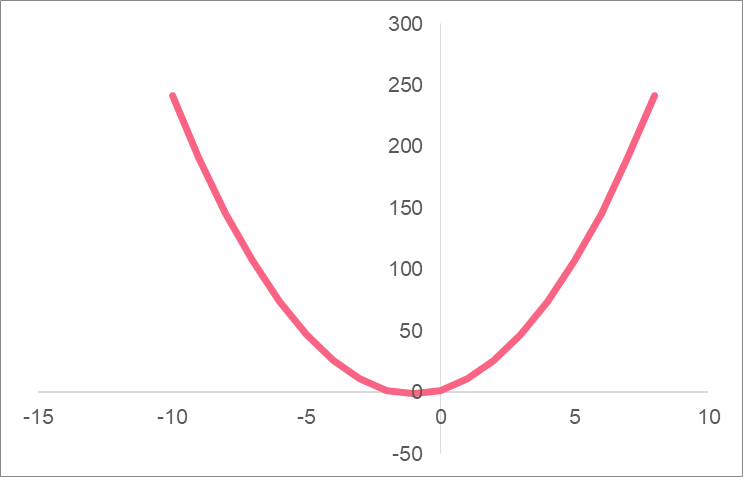
Solution Problem 2
Here is the graph for the following function:

Solution Problem 3
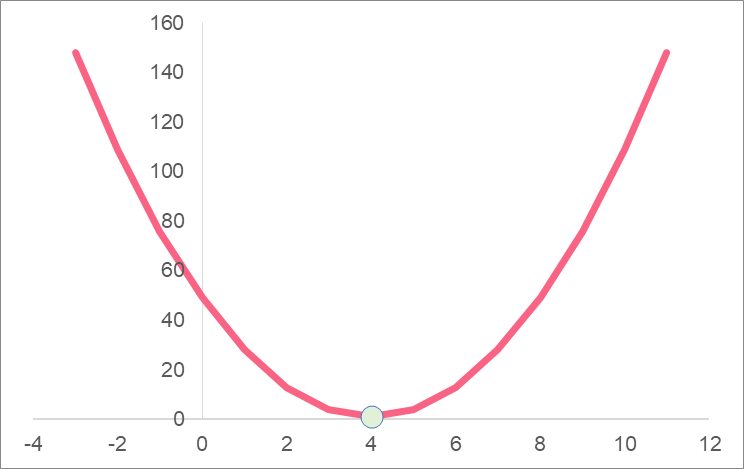
Here we need to use the graph of the quadratic equation in Problem 2. The vertex of this equation is found by looking at the vertex form of the equation and finding (h,k).
The vertex is (4,1). Now, here is the mark on the graph.
Solution Problem 4
Without graphing the function, we can easily tell which one of the following graphs corresponds to the following function:
\[
2x^{3} + 3x
\]
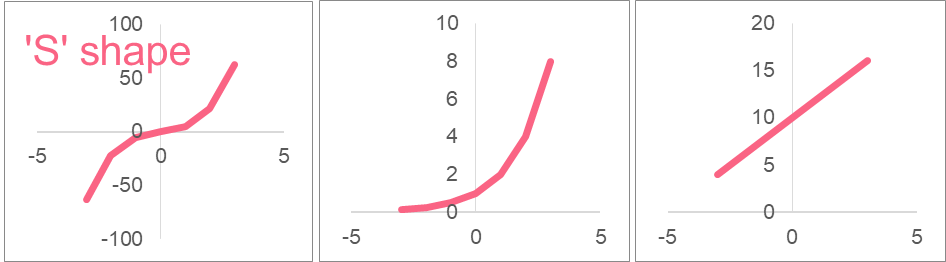
The answer is A. This is because the shape of cubic functions follow an S shape. Because the ‘a’ variable is positive 2, the S shape is backwards.
Solution Problem 5
Here is how you find the function of the line that goes through these two points:
- Point A: (2,5)
- Point B: (6, 7)
\[
m = \frac{7-5}{6-2} = \frac{2}{4} = \frac{1}{2}
\]
The y-intercept is where y = 0.
\[
5 = \frac{1}{2}(2) + b
\]
\[
5 = 1 + b
\]
\[
b = 5 - 1 = 4
\]
\[
y = \frac{1}{2}x + 4
\]
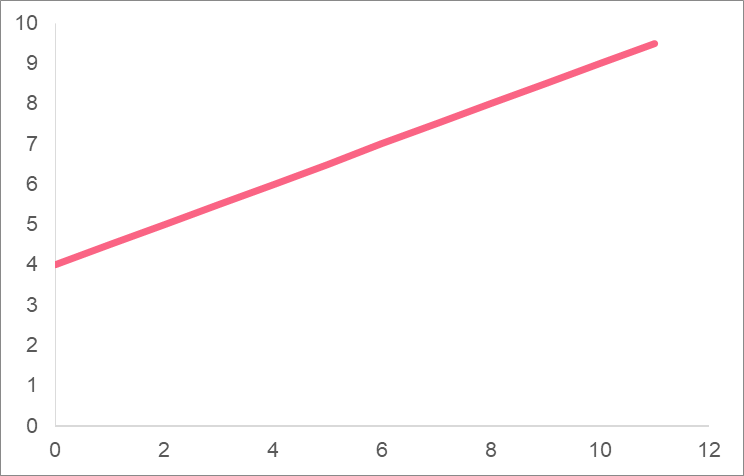
Solution Problem 6
We can transform the following standard form into vertex form using the short cut.
\[
3x^{2} + 6x + 2
\]
\[
h = \frac{-6}{2*3} = -1
\]
\[
k = f(-1) = 3(-1)^{2} + 6(-1) + 2 = 3 - 6 + 2 = -1
\]
\[
Vertex \; form = 3(x + 1)^{2} -1
\]

Summarise with AI:












I have math qstn problm
Break even point