Chapters
There are a few types of sequences and they are:
- Arithmetic Sequence
- Geometric Sequence
- Harmonic Sequence
- Fibonacci Number
There are so many applications of sequences for example analysis of recorded temperatures of anything such as reactor, place, environment, etc. If the record follows a sequence, we can predict the upcoming temperatures which can help us to make the right decision before it's too late. Another example can be paying the loan, some banks follow a sequence of loan payment. You can predict their next loan payment by analyzing the sequence. These are a few examples, there are a lot of applications of sequence. One of the points of interest is convergent and divergent of any sequence. For example, you need to pay your loan to a bank, the bank follows a sequence for the payment and you cleverly identified their sequence. There will be a time when the loan will become zero and that is the point where the sequence converges. After the value becomes zero, as time passes, the value doesn't change (assuming that you never took the loan again). It became zero and it will remain zero forever. When the value becomes stable and doesn't change that indicates that the sequence converges.
Let's say you are a process engineer in an industry. You are observing the temperature of a reactor. You also noted that the temperature of a reactor is changing as time passes and it follows a sequence. You found the equation of that sequence which can help you to predict the temperatures of the reactor. However, the value doesn't converge, it keeps changing as time passes. Hence, we can say that the sequence will go up to infinity. Therefore, we can declare it as a divergent sequence. In simple words, if the sequence doesn't converge to a specific value, that indicates that you are dealing with a divergent sequence. A divergent sequence will have infinite values.

Convergent Sequences
Convergent sequences have a finite limit. It means at a point, the whole series will converge to a single value. For example:
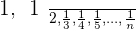
Limit = 0.
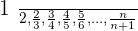
Limit = 1.
Divergent Sequences
Divergent sequences do not have a finite limit.

Limit =  .
.
Oscillating Sequences
Oscillating sequences are not convergent or divergent. Their terms alternate from upper to lower or vice versa.

Alternating Sequences
Alternating sequences change the signs of its terms. They can be:
Convergent
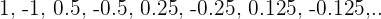
The even and odd terms have a limit of 0.
Divergent
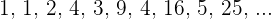
The even and odd terms have limit  .
.
Oscillating

Example
Study the following sequences and determine their type:
1 
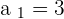
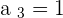

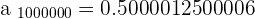
The limit is  .
.
Convergent sequence.
2 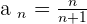

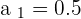
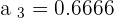
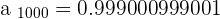
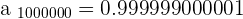
The limit is  .
.
Convergent sequence.













I have math qstn problm
Break even point