Chapters

What is a Logarithm?

| log | Symbol for logarithm |
| a | The base |
| x | Our input |
| y | Our output |
The base of a logarithm helps us answer the following: how many of the number a does it take to get x?

Let’s take an example:

Here, we have the logarithm of 100 with a base of 10. What the logarithm does is tell us how many times we need to multiply the base, 10, to get 100:
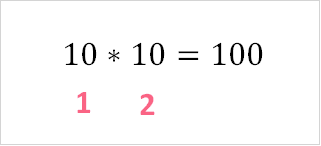
As we can see, the answer is 2. We need to multiply 10 two times to get 100.
Natural Logarithm
The natural logarithm is a special type of logarithm. Take a look at the notation below.

| ln | Symbol for natural log |
| x | Input |
| y | Output |
The natural logarithm as Euler’s number as a base. Take a look below.

As you can see, Euler’s number is approximately 2.72. What exactly does this mean? The natural logarithm means that instead of the base taking on any value we want, it is always e.

Take a look at some examples below.
| ln(5) | 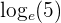 |
| ln(30) | 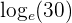 |
| ln(26) |  |
What is an Exponent?
An exponent, also known as a power, says how many times a number should be multiplied by itself. Take a look at the notation below.

Here are a couple of examples.
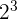 | 2x2x2 |
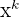 | X multiplied by itself k times |
 | 4 |
Exponents and logarithms are related in that the logarithm tells us what exponent is needed to get a certain value.

Let’s take a look at an example:

Linear Function
In order to understand logarithmic functions, you should be familiar with the concept of functions in general. Functions take a number as input and result in another number as an output.
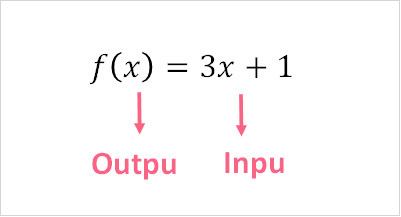
The above is an example of a linear function, which is the most basic function in maths. Let’s try plugging in other values into the function above to get different outputs.
| x | y |
| 1 | 4 |
| 2 | 7 |
| 3 | 10 |
| 4 | 13 |
| 5 | 16 |
When we graph these points, we can see that this function creates a straight line.

This is why linear functions are called ‘linear,’ because the relationship between the input and output of that function is a straight-line relationship.
Logarithmic Function
Logarithmic functions have the same concept as a linear function: they take in a number as input and result in an output. The difference, however, is that the relationship between that input and output is logarithmic instead of linear.

| f(x) | Output |
 | Log with a base of a |
| x | Input |
Let’s take a basic example, with the common base of 10.
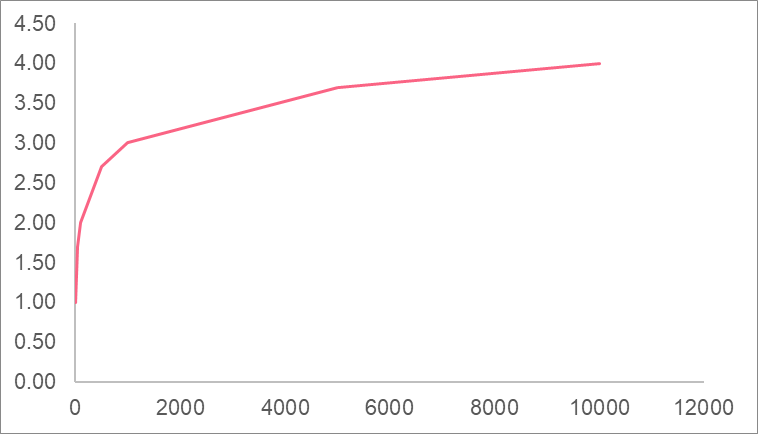
| x | y |
| 10 | 1.00 |
| 50 | 1.70 |
| 100 | 2.00 |
| 500 | 2.70 |
| 1000 | 3.00 |
| 5000 | 3.70 |
| 10000 | 4.00 |
When we plot this on a graph, we get a curved shape, which indicates a logarithmic relationship.
Here are a couple of rules for logarithmic functions:
| When base a between 0 and 1 | 0 < a < 1 | Slope down |
| When base a above 1 | 1 < a | Slope up |
| When base a = 1 | a = 1 | Graph undefined |
Exponential Function
An exponential function is a function that has an exponent in it. Let’s take a look at the notation.

While most functions have the value x as a normal number, exponential functions have x as a power. Let’s take an example.
[
f(x) = 3^{x}
]
| x | y |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
| 4 | 81 |
| 5 | 243 |
| 6 | 729 |
As you can see, while there is only a difference of 5 between x values 1 and 6, there is a difference of more than 700 in their y values. This is typical behaviour of exponential functions, which grow ‘exponentially.’

Natural Log Function
Natural log functions are exactly like log functions, except that instead of any base they have Euler’s number as their base. Take a look at the notation.

Let’s take a look at an example of a natural log function.
[
f(x) = ln(x)
]
| x | y |
| 1 | 0 |
| 2 | 0.69 |
| 4 | 1.39 |
| 20 | 3.00 |
| 100 | 4.61 |
| 150 | 5.01 |

Example 1
Say that you have the following exponential function.
[
f(x) = 1^{x}
]
Try this question out on your own first: what would the graph look like for this function?
In order to answer, let’s start by plugging in some numbers into the function.
| x | y |
| 1 | 1 |
| 2 | 1 |
| 10 | 1 |
| 48 | 1 |
| 100 | 1 |
| 1400 | 1 |
As you can see, 1 to the power of any number is just 1. Therefore, the graph is a horizontal line at 1.

Example 2
You are given the following function’s graph.
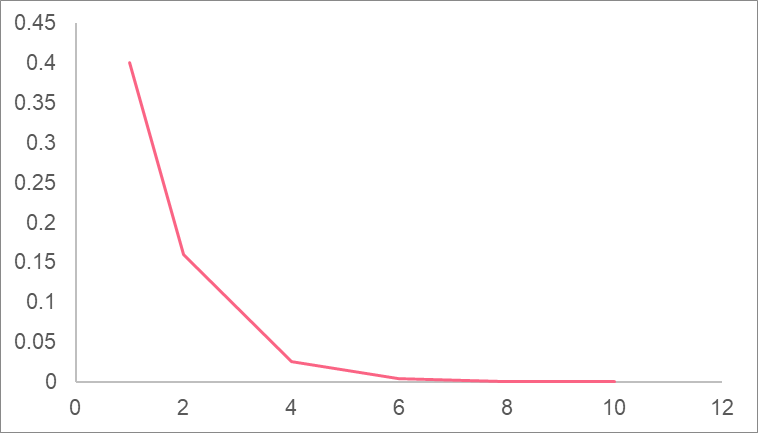
Can you say anything about the a value of the graph just by looking at it? To answer this, recall what the a value is.

For exponential functions, there is a general rule of thumb when it comes to the a value. Take a look at the rules for the value a for any exponential function.
| 0 < a < 1 | Slope down |
| 1 < a | Slope up |
| a = 0 | Graph undefined |
So we can tell even before seeing the function that a is between 0 and 1. The function confirms this:
[
f(x) = 0.4^{x}
]
Summarise with AI:













I have math qstn problm
Break even point