
What are Rational Functions?
A rational function is a type of function which is in form of 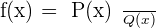 , where
, where 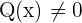 . In simple words, a rational function is a function that is written in a fraction. The
. In simple words, a rational function is a function that is written in a fraction. The  can be a single number or a polynomial. Hence, the criterion is given by a quotient between polynomials:
can be a single number or a polynomial. Hence, the criterion is given by a quotient between polynomials:

The domain is equal to  , minus the values of x that would annul the denominator. What if the
, minus the values of x that would annul the denominator. What if the 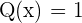 ? Do we still call it rational function? The answer is yes! It also means that every polynomial function is a rational function, how? Make
? Do we still call it rational function? The answer is yes! It also means that every polynomial function is a rational function, how? Make 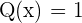 and hence it will become a rational function.
and hence it will become a rational function.
For example,  .
.
We are interested in the denominator because the problem with rational function is that they tend to go to infinity at a point. That is why we make a range for that specific function. The denominator of the above function is  . Make the denominator equal to zero.
. Make the denominator equal to zero.

It means that when x will be equal to 1, the function will reach infinity. Hence we can say that the domain of this function is all the values of x except 1.
Asymptotes
Taking about rational function, the biggest use is in finding asymptotes of the hyperbola. An asymptote is a line that is drawn beside the curve but they both don't touch each other unless they reach infinity. Asymptotes are categorized into three types, horizontal, vertical, and oblique. The functions of the type  has a hyperbola in its graph, however, they look something like this
has a hyperbola in its graph, however, they look something like this 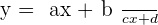 . The simplest hyperbola curve equation is represented like this:
. The simplest hyperbola curve equation is represented like this:  with its asymptotes as axes and the center of the hyperbola is the origin (it is also the point where both asymptotes intersect).
with its asymptotes as axes and the center of the hyperbola is the origin (it is also the point where both asymptotes intersect).
For example, 
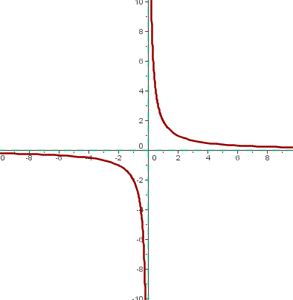
Vertical Translation
In this translation, the vertical asymptote will be shifted according to the equation. In vertical translation, the abscissa will always be zero. Here is the syntax of the equation:

The center of the hyperbola is 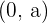 . If
. If  ,
,  moves upward "a" units. For example:
moves upward "a" units. For example:


The center of the hyperbola is: 
If  ,
,  moves downwards "a" units. For example:
moves downwards "a" units. For example:

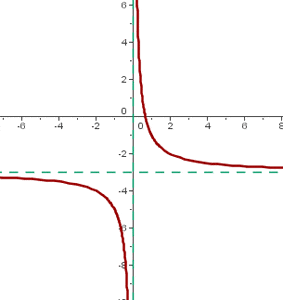
The center of the hyperbola is: 
Horizontal Translation
For the case of horizontal translation, the asymptote shifts horizontally according to the equation. In horizontal translation, the ordinate will always be zero. Below is the syntax of the equation:

The center of the hyperbola is: 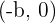 . Do note the minus sign in the center coordinates of the hyperbola, this is a very common mistake.
. Do note the minus sign in the center coordinates of the hyperbola, this is a very common mistake.
If 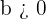 ,
,  is shifted to the left "b" units. For example:
is shifted to the left "b" units. For example:
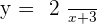

The center of the hyperbola is: 
If 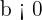 ,
,  is shifted to the right "b" units. For example:
is shifted to the right "b" units. For example:

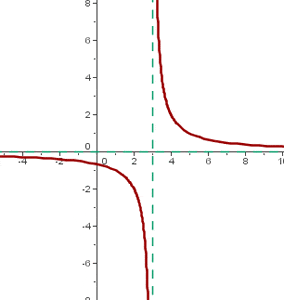
The center of the hyperbola is: 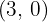
Oblique Translation
The oblique translation consists of two translation at the same time. The horizontal and vertical translations. Here is the syntax of the equation:
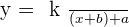
Neither of the coordinates can be zero under the oblique translation condition. The center of the hyperbola is  . For example:
. For example:
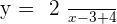
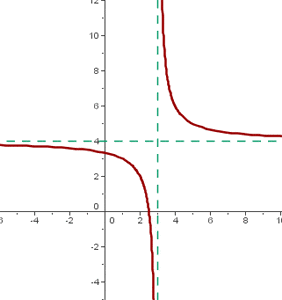
The center of the hyperbola is:  .
.
Graphing Hyperbolas
Remember, we told you that the hyperbola equation looks something like this in reality:
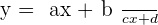
It is modified and then written as
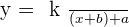
Where "a" and "b" determines the point where both asymptotes meet each other. Its graph is a hyperbola with a center (−b, a) and asymptotes parallel to the axes.
Example
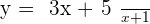

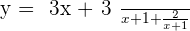

Compare it to 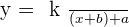


Remember, the center is written as: 
The center of the hyperbola is: 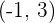 .
.












I have math qstn problm
Break even point