Chapters
A function can be made with many pieces. For example, after some certain values, the function can change its shape and once it changes its shape that means a change in the equation. The pieces have no specific limit, which means that a function can have many pieces. Since the function has pieces that is why we call it a piecewise function. The piecewise functions are functions defined by different criteria according to the intervals being considered. For example:
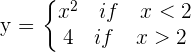
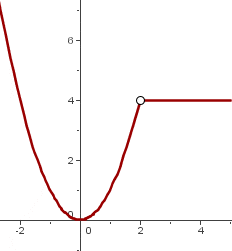
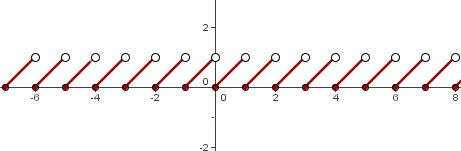
Looking at the above graph, we can conclude a few things. Firstly, we observed that there are two different shapes, which means that we are dealing with two different pieces but within the same domain. Secondly, the breakpoint is  which means that there is a shift in the equation at point
which means that there is a shift in the equation at point  . When
. When 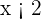 , the graph was following the equation
, the graph was following the equation 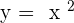 hence you will see the graph of equation
hence you will see the graph of equation 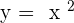 from infinity to
from infinity to  . However, at
. However, at  , things are about to change, the graph is following the equation
, things are about to change, the graph is following the equation  , and since
, and since  has no limit, it will continue till infinity.
has no limit, it will continue till infinity.
Domain of y: 

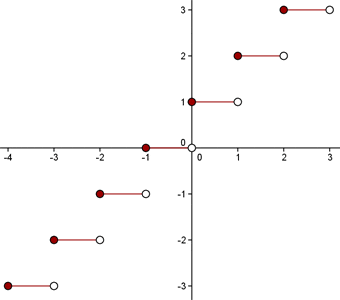
Floor Function
The floor function or greatest integer function gives the largest integer less than or equal to x. For example, you are asked to figure out the floor function of 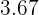 , now you need to find the greatest integer that is less than
, now you need to find the greatest integer that is less than 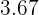 . Some of you might be thinking the largest integer less than
. Some of you might be thinking the largest integer less than 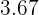 will be
will be  and that is where you are wrong, we are talking about integers here. Hence, the largest integer which is less than
and that is where you are wrong, we are talking about integers here. Hence, the largest integer which is less than 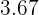 will be
will be  .
.

 |  |  | 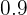 |  |  |  |  |
 |  |  |  |  |  |  |  |
|---|

Ceiling Function
The ceiling function or least integer function gives the smallest integer greater than or equal to x. For example, we will take the above example again but with a small change, this time you were asked to figure out the ceiling function of 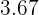 . The answer is
. The answer is  because
because  is the least integer which is greater than
is the least integer which is greater than 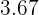 .
.

 |  |  | 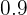 |  |  |  |  |
 |  |  |  |  |  |  |  |
|---|

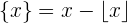
 |  |  | 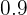 |  |  |  |  |
|---|---|---|---|---|---|---|---|
 |  |  | 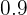 |  |  | 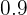 |  |

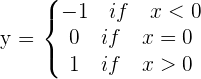














I have math qstn problm
Break even point