Chapters

Linear Function Definition
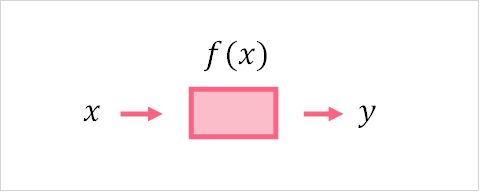
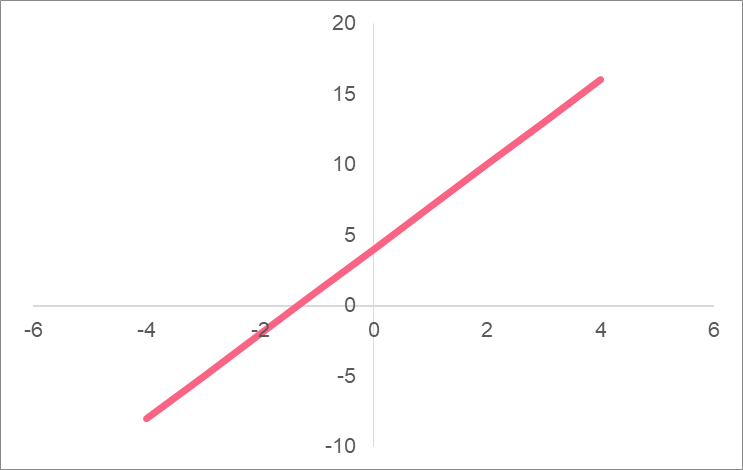
| x | f(x) |
| ... | ... |
| -1 | 1 |
| 0 | 4 |
| 1 | 7 |
| ... | ... |
What you can see in this graph is a linear function. Here is the standard way to write a linear function.

| f(x) | Read as ‘f of x’ and can be thought of as y |
| m | The slope |
| x | The input |
| b | The y-intercept |
When we use functions, we use f of x, written as f(x), which can be thought of as what we usually call y. The linear function we used above can be written as:

Radicals
A radical function is any function that includes radicals. In algebra, radicals are also called roots. You may be familiar with how they look like:
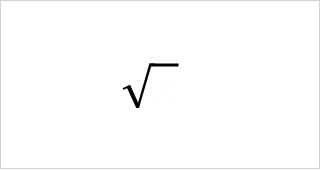
This symbol is quite powerful - let’s take a look at a few examples of radicals to see why.
| Name | Example | |
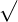 , , 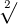 | Square root, square | 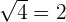 |
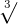 | Cube root, cubic | 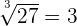 |
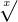 | Root | 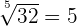 |
A radical function, then, is simply a function that takes any number as an input and takes a root of it. Let’s take a basic example:

The number inside of a square root, so we can plug in any number greater or equal to zero.
| x | f(x) |
| 0 | 0.0 |
| 1 | 1.0 |
| 2 | 1.4 |
| 3 | 1.7 |
| ... | ... |
We can keep going, plotting each output up to 21. Next, we can graph the result.
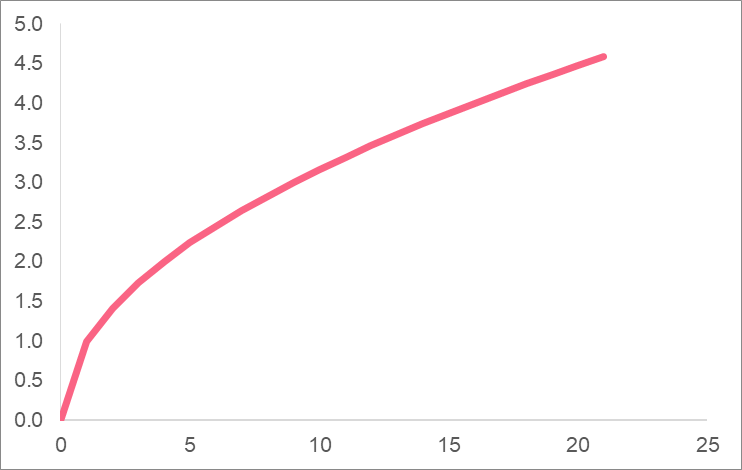
As you can see, the graph of a radical function is quite different from a linear function. Take a look at some more examples below.
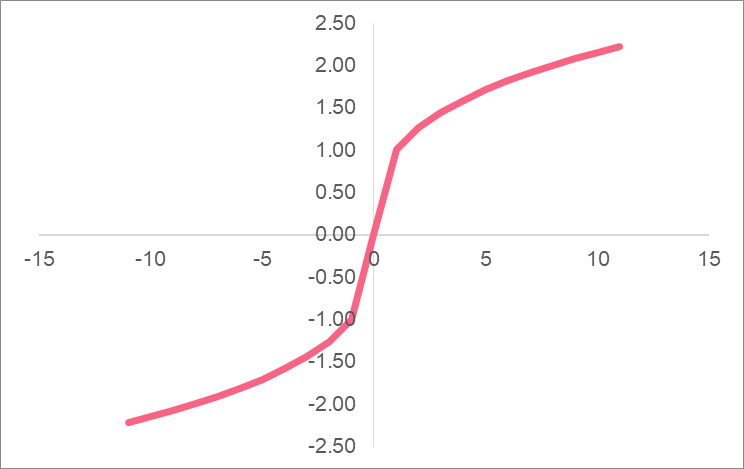
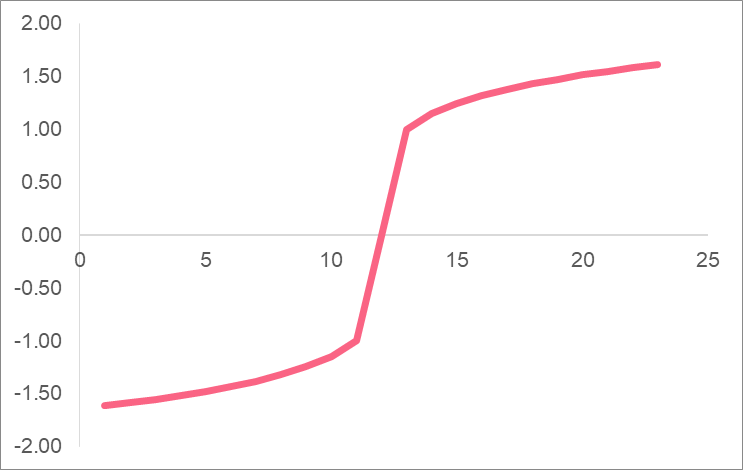
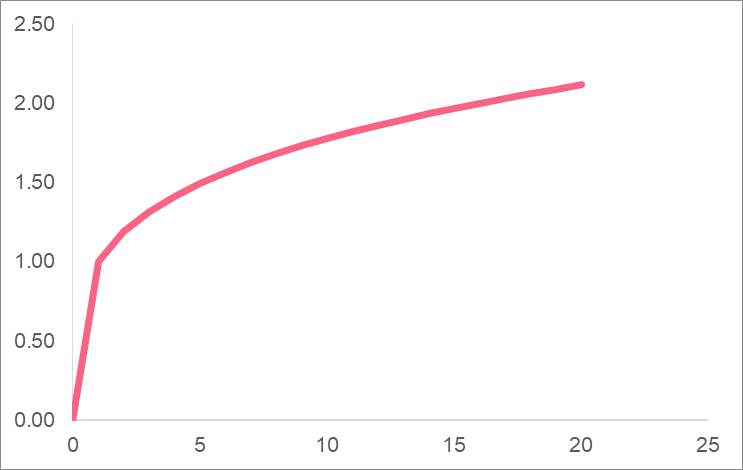
Power Function
A power function is a function that involves a power. A power is also known as taking a number to the nth power. Take a look at the image below to get a better understanding.

As you can see, we have a couple of elements involved here. The table below explains each element in the power function.
| k | Constant | 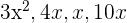 |
| x | Variable | x,y,z,etc. |
| n | Power | 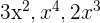 |
When you’re using power functions, you will probably come across two terms:
- Growth function
- Decay function
These two functions are found in many different disciplines and are usually used to model things with an exponential relationship. An exponential relationship is one modelled by an exponent, also known as a power. Take a look at a simple exponent relationship below.
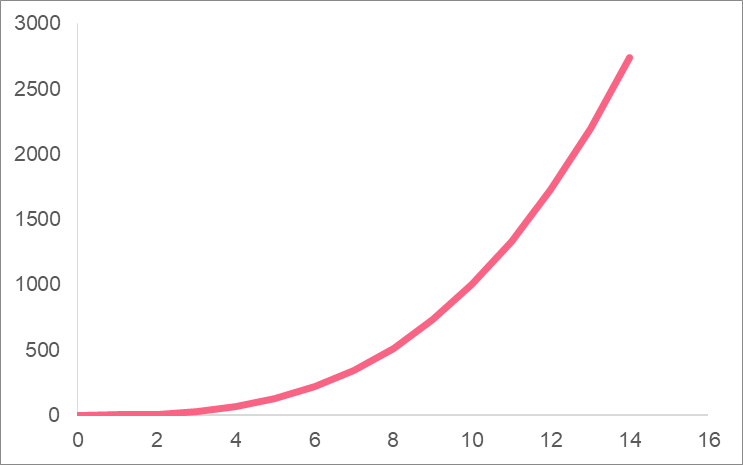
As you can see, ‘growth’ happens super quickly. While there’s not that much of a difference between 3 numbers, the difference between 9 to the power of 3 and 10 to the power of 3 is almost 300.
Radical and Power Rules
There are many rules when it comes to radicals and powers. First, let’s focus on radical rules. Take a look at the table below to get an idea of the rules and examples for each rule.
| Rule | Example | |
| 1 | 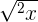 = =  | 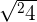 = = 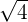 |
| 2 | 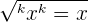 | 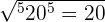 |
| 3 | 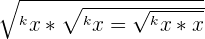 | 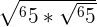 = = 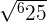 |
Now that you understand a bit more about radical rules, let’s take a look at some rules for powers.
| Rule | Example | |
| 1 | 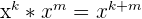 | 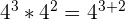 |
| 2 | 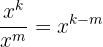 | 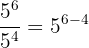 |
| 3 | 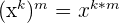 | 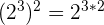 |
| 4 | 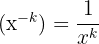 | 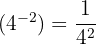 |
| 5 | 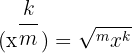 | 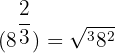 |
Step-by-Step Factoring Radicals
Now that you’ve learned about radicals and how they relate to powers, let’s take a look at an example where we will factor a radical step-by-step. First, we will start with an easier example. The three examples after this one build upon each other.
Take a look at the radical below.
\[
\sqrt^{3}{(2^{5})*(2^{-2})}
\]
While this may look complex at first, we can start by focusing on what is inside of the fraction. The first step in simplifying this radical is to recall that negative exponents mean we have to take the inverse of the number.
\[
\sqrt^{3}{(2^{5})*(\frac{1}{2^{2}})}
\]
Next, since we are multiplying a whole number by a fraction, we can rewrite that into one simple fraction.
\[
\sqrt^{3}{ \frac{ (2^{5}) }{ (2^{2}) } }
\]
Now, we can see that since we have the same main number in the numerator and the denominator, we can use the power rules to simplify this fraction.
\[
\sqrt^{3}{ 2^{5-2} } = \sqrt^{3}{ 2^{3} } = 2
\]
Since the nth square root of a number to the nth power is just the number, we can stop here and say the answer is 2.
Example 1
In this example, try to simplify the radical below by yourself first. Then, compare your solution with the following.

Take a look at the step-by-step solution below.
\[
\sqrt^{3}{2^{4} * \frac{1}{\sqrt^{3}{8}}}
\]
\[
\sqrt^{3}{2^{4} *\frac{1}{2}}
\]
\[
\sqrt^{3}{\frac{2^{4}}{2}}
\]
\[
\sqrt^{3}{2^{4-1}} = \sqrt^{3}{2^{3}} = 2
\]
Example 2
In this example, try to simplify the radical below by yourself first. Then, compare your solution with the following.

Take a look at the step-by-step solution below.
\[
\sqrt^{3}{250}
\]
\[
\sqrt^{3}{125*2}
\]
\[
\sqrt^{3}{125} * \sqrt^{3}{2}
\]
\[
5(\sqrt^{3}{2})
\]
Example 3
In this example, try to simplify the radical below by yourself first. Then, compare your solution with the following.

Take a look at the step-by-step solution below.
\[
(\sqrt{74})^{6}
\]
\[
(74^{1/2})^{6}
\]
\[
74^{1/2*6} = 74^{3}
\]













I have math qstn problm
Break even point