Chapters
- Calculate the Intervals of Increase and Decrease for the Following Functions:
- Exercise 1
- Exercise 2
- Exercise 3
- Exercise 4
- Exercise 5
- Exercise 6
- Exercise 7
- Exercise 8
- Exercise 9
- Exercise 10
- Exercise 11
- Exercise 12
- Exercise 13
- Exercise 14
- Exercise 15
- Exercise 16
- Exercise 17
- Solution of exercise 1
- Solution of exercise 2
- Solution of exercise 3
- Solution of exercise 4
- Solution of exercise 5
- Solution of exercise 6
- Solution of exercise 7
- Solution of exercise 8
- Solution of exercise 9
- Solution of exercise 10
- Solution of exercise 11
- Solution of exercise 12
- Solution of exercise 13
- Solution of exercise 14
- Solution of exercise 15
- Solution of exercise 16
- Solution of exercise 17

The best Maths tutors available
Calculate the Intervals of Increase and Decrease for the Following Functions:
Exercise 1
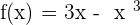
Exercise 2
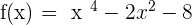
Exercise 3
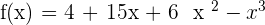
Exercise 4

Exercise 5
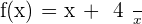
Exercise 6
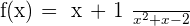
Exercise 7
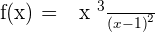
Exercise 8

Exercise 9
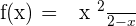
Exercise 10
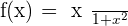
Exercise 11

Exercise 12
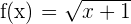
Exercise 13
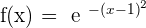
Exercise 14
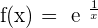
Exercise 15
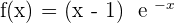
Exercise 16
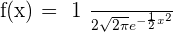
Exercise 17
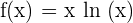
Solution of exercise 1
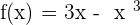

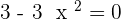
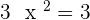


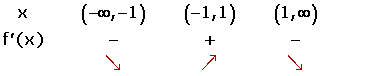
Increasing:

Decreasing:

Solution of exercise 2
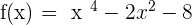
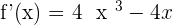
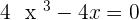

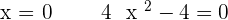
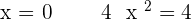



Increasing: 
Decreasing: 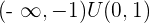
Solution of exercise 3
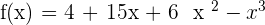


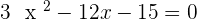


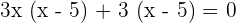
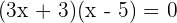



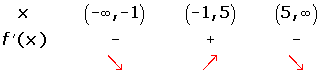
Increasing: 
Decreasing: 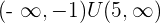
Solution of exercise 4


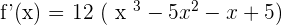
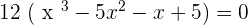

After solving the cubic equation, we will get:
 {}^{}
{}^{}
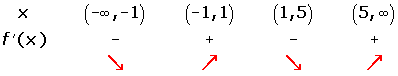
Increasing: 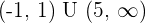
Decreasing: 
Solution of exercise 5
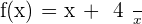


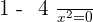
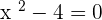
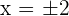
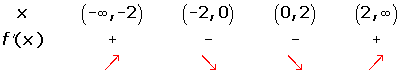
Increasing: 
Decreasing: 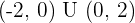
Solution of exercise 6

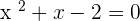
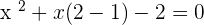
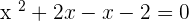
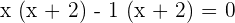




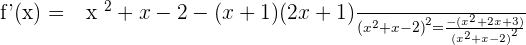

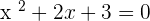
No solutions in 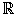

Decreasing: 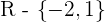
Solution of exercise 7
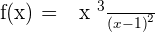
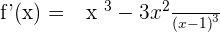
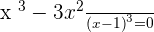



Increasing: 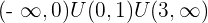
Decreasing: 
Solution of exercise 8

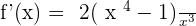

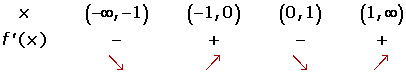
Increasing: 
Decreasing: 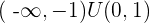
Solution of exercise 9
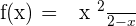

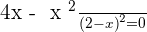

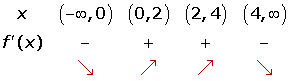
Increasing: 
Decreasing: 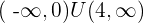
Solution of exercise 10
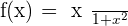

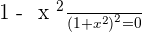



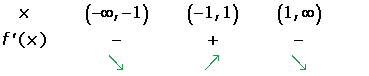
Increasing: 
Decreasing: 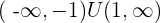
Solution of exercise 11

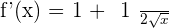

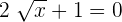
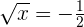
Hence we got no solution

Increasing: 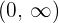
Solution of exercise 12
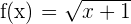
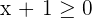

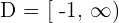

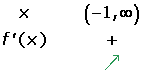
Increasing: 
Solution of exercise 13
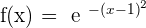
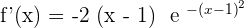
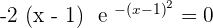


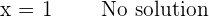
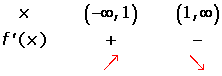
Increasing: 
Decreasing: 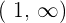
Solution of exercise 14
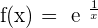
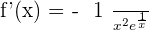

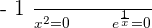
Both solutions can't be solved
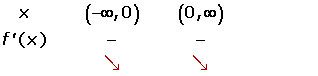
Decreasing: 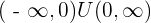
Solution of exercise 15
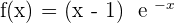
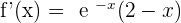
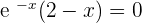
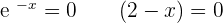
 is the only possible solution
is the only possible solution

Increasing: 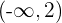
Decreasing: 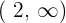
Solution of exercise 16

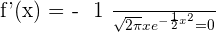
 is the only possible solution
is the only possible solution

Increasing: 
Decreasing: 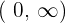


Solution of exercise 17
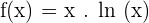
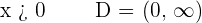
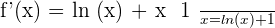
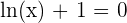
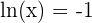

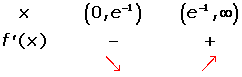
Increasing: 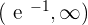
Decreasing: 
Summarise with AI:












I have math qstn problm
Break even point